Вначале вспомним, что такое координатная ось , проекция точки на ось и координаты точки на оси .
Координатная ось - это прямая, которой придается какое-то направление. Можете считать, что это вектор с бесконечно большим модулем.
Координатная ось обозначается какой-либо буквой: X , Y , Z , s , t … Обычно на оси выбирается (произвольно) точка, которая называется началом отсчета и, как правило, обозначается буквой О. От этой точки отсчитываются расстояния до других интересующих нас точек.
Проекция точки на ось - это основание перпендикуляра, опущенного из этой точки на данную ось (рис. 8). То есть, проекцией точки на ось является точка.
Координата точки на ось - это число, абсолютная величина которого равна длине отрезка оси (в выбранном масштабе), заключённого между началом оси и проекцией точки на эту ось. Это число берется со знаком плюс, если проекция точки располагается в направлении оси от ее начала и со знаком минус, если в противоположном направлении.
Скалярная проекция вектора на ось - это число , абсолютная величина которого равна длине отрезка оси (в выбранном масштабе), заключённого между проекциями точки начала и точки конца вектора. Важно! Обычно вместо выражения скалярная проекция вектора на ось говорят просто - проекция вектора на ось , то есть слово скалярная опускают. Проекция вектора обозначается той же буквой, что и проектируемый вектор (в обычном, нежирном написании), с нижним (как правило) индексом названия оси, на которую этот вектор проектируется. Например, если на ось Х проектируется вектор а, то его проекция обозначается а x . При проектировании этого же вектора на другую ось, скажем, ось Y , его проекция будет обозначаться а y (рис. 9).

Чтобы вычислить проекцию вектора на ось (например, ось X) надо из координаты точки его конца вычесть координату точки начала, то есть
а x = х к − x н.
Надо помнить: скалярная проекция вектора на ось (или, просто, проекция вектора на ось) - это число (не вектор)! Причем, проекция может быть положительной, если величина х к больше величины х н, отрицательной, если величина х к меньше величины х н и равной нулю, если х к равно х н (рис. 10).

Проекцию вектора на ось можно также найти, зная модуль вектора и угол, который он составляет с этой осью.
Из рисунка 11 видно, что а x = а Cos α
То есть, проекция вектора на ось равна произведению модуля вектора на косинус угла между направлением оси и направлением вектора . Если угол острый, то Cos α > 0 и а x > 0, а, если тупой, то косинус тупого угла отрицателен, и проекция вектора на ось тоже будет отрицательна.

Углы, отсчитываемые от оси против хода часовой стрелки, принято считать положительными, а по ходу - отрицательными. Однако, поскольку косинус - функция четная, то есть, Cos α = Cos (− α), то при вычислении проекций углы можно отсчитывать как по ходу часовой стрелки, так и против.
При решении задач часто будут использоваться следующие свойства проекций: если
а = b + c +…+ d , то а x = b x + c x +…+ d x (аналогично на другие оси),
a = mb , то а x = mb x (аналогично на другие оси).
Формула а x = а Cos α будет очень часто встречаться при решении задач, поэтому ее обязательно надо знать. Правило определения проекции надо знать наизусть!
Запомните!
Чтобы найти проекцию вектора на ось надо модуль этого вектора умножить на косинус угла между направлением оси и направлением вектора.
Еще раз - НАИЗУСТЬ!
Векторное описание движения является полезным, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения. Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами – проекциями векторов.
Проекцией вектора на ось называют скалярную величину, равную произведению модуля проектируемого вектора на косинус угла между направлениями вектора и выбранной координатной оси.
На левом чертеже показан вектор перемещения, модуль которого 50 км, а его направление образует тупой угол 150° с направлением оси X. Пользуясь определением, найдём проекцию перемещения на ось X:
sx = s · cos(α) = 50 км · cos( 150°) = –43 км
Поскольку угол между осями 90°, легко подсчитать, что направление перемещения образует с направлением оси Y острый угол 60°. Пользуясь определением, найдём проекцию перемещения на ось Y:
sy = s · cos(β) = 50 км · cos( 60°) = +25 км
Как видите, если направление вектора образует с направлением оси острый угол, проекция положительна; если направление вектора образует с направлением оси тупой угол, проекция отрицательна.
На правом чертеже показан вектор скорости, модуль которого 5 м/с, а направление образует угол 30° с направлением оси X. Найдём проекции:
υx = υ · cos(α) = 5 м/c · cos( 30°) = +4,3 м/с
υy = υ · cos(β) = 5 м/с · cos( 120°) = –2,5 м/c
Гораздо проще находить проекции векторов на оси, если проецируемые векторы параллельны или перпендикулярны выбранным осям. Обратим внимание, что для случая параллельности возможны два варианта: вектор сонаправлен оси и вектор противонаправлен оси, а для случая перпендикулярности есть только один вариант.
Проекция вектора, перпендикулярного оси, всегда равна нулю (см. sy и ay на левом чертеже, а также sx и υx на правом чертеже). Действительно, для вектора, перпендикулярного оси, угол между ним и осью равен 90°, поэтому косинус равен нулю, значит, и проекция равна нулю.

Проекция вектора, сонаправленного с осью, положительна и равна его модулю, например, sx = +s (см. левый чертёж). Действительно, для вектора, сонаправленного с осью, угол между ним и осью равен нулю, и его косинус «+1», то есть проекция равна длине вектора: sx = x – xo = +s .
Проекция вектора, противонаправленного оси, отрицательна и равна его модулю, взятому со знаком «минус», например, sy = –s (см. правый чертёж). Действительно, для вектора, противонаправленного оси, угол между ним и осью равен 180°, и его косинус «–1», то есть проекция равна длине вектора, взятой с отрицательным знаком: sy = y – yo = –s .
На правых частях обоих чертежей показаны другие случаи, когда векторы параллельны одной из координатных осей и перпендикулярны другой. Предлагаем вам убедиться самостоятельно, что и в этих случаях тоже выполняются правила, сформулированные в предыдущих абзацах.
а. Проекцией точки А на ось PQ (рис. 4) называется основание а перпендикуляра, опущенного из данной точки на данную ось. Та ось, на которую мы проектируем, называется осью проекций.
Ь. Пусть даны две оси и вектор А В, указанные на рис. 5.

Вектор началом которого служит проекция начала и концом - проекция конца данного вектора, называется проекцией вектора А В на ось PQ, Записывается это так;
![]()
Иногда указатель PQ внизу не пишется, это делается в тех случаях, когда кроме PQ нет другой осиг на которую можно было бы проектировать.
с. Теорема I. Величины векторов, лежащих на одной оси, относятся как величины их проекций на любую ось.

Пусть даны оси и векторы, указанные на рис, 6. Из подобия треугольников видно, что длины векторов относятся, как длины их проекций, т. е.
![]()
Так как векторы на чертеже направлены в разные стороны, то величины их имеют различный внак, следовательно,
![]()
Очевидно, величины проекций также имеют различный знак:
![]()
подставляя (2) в (3) в (1), получим
![]()
Меняя знаки на обратные, получим
![]()
Если векторы будут одинаково направлены, то будут одного направления и их проекции; в формулах (2) и (3) знаков минус не будет. Подставляя (2) и (3) в равенство (1), мы сразу получим равенство (4). Итак, теорема доказана для всея случаев.

d. Теорема II. Величина проекции вектора на любую ось равна величине вектора, умножен» ной на косинус угла между осью проекций и осью вектора, Пусть даны оси вектор как указано на рис. 7. Построим вектор одинаково направленный со своей осью и отложенный, например, от точки пересечения осей. Пусть длина его равна единице. Тогда и величина его
![]()
Ответ:
Свойства проекций:
Свойства проекции вектора
Свойство 1.
Проекция суммы двух векторов на ось равна сумме проекций векторов на ту же ось: ![]()
Это свойство позволяет заменять проекцию суммы векторов суммой их проекций и наоборот.
Свойство 2. Если вектор умножается на число λ, то его проекция на ось также умножается на это число:
![]()
Свойство 3.
Проекция вектора на ось l равна произведению модуля вектора на косинус угла между вектором и осью:
Орт оси. Разложение вектора по координатным ортам. Координаты вектора. Свойства координат
Ответ:
Орты осей.

Прямоугольная система координат (любой размерности) также описывается набором ортов, сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу.
В трёхмерном случае орты обычно обозначаются
И Могут также применяться обозначения со стрелками и
При этом в случае правой системы координат действительны следующие формулы с векторными произведениями ортов:
Разложение вектора по координатным ортам.
Орт координатной оси обозначается через , оси - через , оси - через (рис. 1)

Для любого вектора который лежит в плоскости имеет место следующее разложение:
Если вектор ![]() расположен в пространстве, то разложение по ортам координатных осей имеет вид:
расположен в пространстве, то разложение по ортам координатных осей имеет вид:
Координаты вектора:
Чтобы вычислить координаты вектора, зная координаты (x1; y1) его начала A и координаты (x2; y2) его конца B, нужно из координат конца вычесть координаты начала: (x2 – x1; y2 – y1).
Свойства координат.
Рассмотрим координатную прямую с началом координат в точке О и единичным вектором i. Тогда для любого вектора a на этой прямой: a = axi.
Число ax называется координатой вектора a на координатной оси.
Свойство 1. При сложении векторов на оси их координаты складываются.
Свойство 2. При умножении вектора на число его координата умножается на это число.
Скалярное произведение векторов. Свойства.
Ответ:
Скалярным произведением двух ненулевых векторов называется число,
равное произведению этих векторов на косинус угла между ними.
![]()
![]()
Свойства:
1. Скалярное произведение обладает переместительным свойством: ab=bа

Скалярное произведение координатных ортов. Определение скалярного произведения векторов, заданных своими координатами.
Ответ:
Скалярное произведение (×) орты
| (X) | I | J | K |
| I | |||
| J | |||
| K |
Определение скалярного произведения векторов, заданных своими координатами.
Скалярное произведение двух векторов и заданных своими координатами, может быть вычислено по формуле
![]()
Векторное произведение двух векторов. Свойства векторного произведения.
Ответ:
Три некомпланарных вектора образуют правую тройку если с конца третьего поворот от первого вектора ко второму совершается против часовой стрелки. Если по часовой – то левую., если нет то в противоположном (показать как он показывал с «ручками»)
Векторным произведением вектора а на векторb называется вектор с который:
1. Перпендикулярен векторам а иb
2. Имеет длину, численно равную площади параллелограмма, образованного на a и b векторах
![]()
3. Векторы, a ,b , и c образуют правую тройку векторов
Свойства:
1. ![]()
3. ![]()
4. ![]()

Векторное произведение координатных ортов. Определение векторного произведения векторов, заданных своими координатами.
Ответ:
Векторное произведение координатных ортов.

Определение векторного произведения векторов, заданных своими координатами.
Пусть векторы а = (х1; у1; z1) и b = (х2; у2; z2) заданы своими координатами в прямоугольной декартовой системе координат О, i, j, k, причем тройка i, j, k является правой.
Разложим а и b по базисным векторам:
а = x 1 i + y 1 j + z 1 k, b = x 2 i + y 2 j + z 2 k.
Используя свойства векторного произведения, получаем
[а; b] = =
= x 1 x 2 + x 1 y 2 + x 1 z 2 +
+ y 1 x 2 + y 1 y 2 + y 1 z 2 +
+ z 1 x 2 + z 1 y 2 + z 1 z 2 . (1)
По определению векторного произведения находим
= 0, = k, = - j,
= - k, = 0, = i,
= j, = - i. = 0.
Учитывая эти равенства, формулу (1) можно записать так:
[а; b] = x 1 y 2 k - x 1 z 2 j - y 1 x 2 k + y 1 z 2 i + z 1 x 2 j - z 1 y 2 i
[а; b] = (y 1 z 2 - z 1 y 2) i + (z 1 x 2 - x 1 z 2) j + (x 1 y 2 - y 1 x 2) k. (2)
Формула (2) дает выражение для векторного произведения двух векторов, заданных своими координатами.
Полученная формула громоздка.Используя обозначения определителей можно записать ее в другом более удобном для запоминания виде:
Обычно формулу (З) записывают еще короче:

По
физике
за 9 класс (И.К.Кикоин, А.К.Кикоин, 1999 год),
задача №5
к главе «ГЛАВА 1. ОБЩИЕ СВЕДЕНИЯ О ДВИЖЕНИИ
».
1. Что называют проекцией вектора на координатную ось?
1. Проекцией вектора а на координатную ось называют длину отрезка между проекциями начала и конца вектора а (перпендикулярами, опущенными из этих точек на ось) на эту координатную ось.
2. Как связан вектор перемещения тела с его координатами?
2. Проекции вектора перемещения s на оси координат равны изменению соответствующих координат тела.
3. Если координата точки с течением времени увеличивается, то какой знак имеет проекция вектора перемещения на координатную ось? А если она уменьшается?
3. Если координата точки с течением времени увеличивается, то проекция вектора перемещения на координатную ось будет положительной, т.к. в этом случае мы будем идти от проекции начала к проекции конца вектора по направлению самой оси.
Если координата точки с течением времени будет уменьшаться, то проекция вектора перемещения на координатную ось будет отрицательной, т.к. в этом случае мы будем идти от проекции начала к проекции конца вектора против направляющей самой оси.
4. Если вектор перемещения параллелен оси X, то чему равен модуль проекции вектора на эту ось? А модуль проекции этого же вектора на ось У?
4. Если вектор перемещения параллелен оси Х, то модуль проекции вектора на эту ось равен модулю самого вектора, а его проекция на ось Y равна нулю.
5. Определите знаки проекций на ось X векторов перемещения, изображенных на рисунке 22. Как при этих перемещениях изменяются координаты тела?
5. Во всех нижеследующих случаях координата Y тела не изменяется, а координата Х тела будет изменяться следующим образом:
a) s 1 ;
проекция вектора s 1 , на ось Х отрицательна и по модулю равна длине вектора s 1 . При таком перемещении координата Х тела уменьшится на длину вектора s 1 .
b) s 2 ;
проекция вектора s 2 на ось X положительна и равна по модулю длине вектора s 1 . При таком перемещении координата Х тела увеличится на длину вектора s 2 .
c) s 3 ;
проекция вектора s 3 на ось Х отрицательна и равна по модулю длине вектора s 3 . При таком перемещении координата Х тела уменьшится на длину вектора s 3 .
d) s 4 ;
проекция вектора s 4 на ось X положительна и равна по модулю длине вектора s 4 . При таком перемещении координата Х тела увеличится на длину вектора s 4 .
e) s 5 ;
проекция вектора s 5 на ось Х отрицательна и равна по модулю длине вектора s 5 . При таком перемещении координата Х тела уменьшится на длину вектора s 5 .
6. Если значение пройденного пути велико, то может ли модуль перемещения быть малым?
6. Может. Это связано с тем, что перемещение (вектор перемещения) является векторной величиной, т.е. представляет собой направленный отрезок прямой, соединяющий начальное положение тела с его последующими положениями. А конечное положение тела (вне зависимости от величины пройденного пути) может находиться как угодно близко к первоначальному положению тела. В случае совпадения конечного и начального положений тела, модуль перемещения будет равен нулю.
7. Почему в механике более важен вектор перемещения тела, чем пройденный им путь?
7. Основной задачей механики является определение положения тела в любой момент времени. Зная вектор перемещения тела мы можем определить координаты тела, т.е. положение тела в любой момент времени, а зная только пройденный путь мы не можем определить координаты тела, т.к. мы не имеем сведений о направлении движения, а можем только судить о длине пройденного пути на данный момент времени.

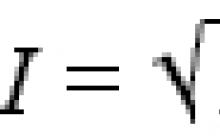








«плюсы» и«минусы» демократии
Геодезист. Кто такой геодезист? Описание профессии. Профессия геодезист Геодезист обучение
Магеллановы облака: кто они?
Перечный соус для стейка Сливочный перечный соус
Как составить грамотное портфолио дизайнеру